Caso No. 03: Dinámica de Poblaciones

Comencemos con nuestra tercera sesión de conclusiones, el tema a tratar esta semana es: la dinámica de poblaciones. Comencemos, como ya es costumbre hacerlo, definiendo el primer pilar de nuestras conclusiones: la dinámica de poblaciones es el estudio de la velocidad con que cambia la cantidad de individuos de una población. Ahora bien, lo que a nosotros nos concierne, además de la parte dinámica de esta rama, es la forma en que se modelan estas poblaciones a estudiar.

Evidentemente, por ser el objetivo cuantificar la velocidad con que varía un sistema, un modelo de este tipo se basa en el clásico concepto del balance de cantidades. Antes de comenzar a plantear modelos, será conveniente “aterrizar” un par de ideas para después generalizarlas a poblaciones. Comencemos con un ejemplo sencillo, pero demasiado bien definido, de un proceso discontinuo. Imagínese, querido lector, que usted acaba de beber un litro de agua para saciar la sed y que es de nuestro interés estimar la cantidad del vital líquido que permanece dentro de su organismo durante un intervalo de tiempo definido.

Su intuición debe hacerle pensar en un par de cosas, que debería saber por costumbre: 1) el agua que acaba de ingerir modifica la cantidad de líquido que tenía en su cuerpo y 2) cuando usted “desbebe” está nuevamente alterando la cantidad de líquido en su cuerpo. Ahora bien, cómo podemos determinar la cantidad de agua que tenemos dentro de nuestro organismo? Si bien no podemos determinar de manera exacta la cantidad de líquido dentro de nuestro organismo, incluso antes de tomar ese refrescante litro de agua, podemos saber cómo varía la cantidad de agua dentro de nuestro organismo.

Vamos a crear un modelo sencillo que represente esta variación. Tenemos, para comenzar, una entrada (ingesta de agua) y una salida de agua (la acción de “desbeber”). Si la cantidad de agua dentro de nuestro cuerpo no se viera afectada, deberíamos establecer que toda el agua que entra sale, es decir:

Pero cómo sabemos que parte de esa agua queda dentro de nuestro organismo (si no, para qué ver la parte dinámica?) necesitamos incluir un tercer término: la acumulación de agua dentro de nuestro organismo. Es lógico pensar que si tomamos dos litros de agua y “des-tomamos” un litro nada más, tenemos un litro extraviado que debe haberse quedado en algún lugar dentro de nuestro cuerpo, o mejor dicho, que se acumuló en nuestro cuerpo. Por lo tanto, matemáticamente:

Nuestro modelo comienza a tomar forma pero aún le faltan un par de términos. Imagínese ahora que está sentado (leyendo el blog de un servidor, para hacer más agradables las cosas) expuesto a una temperatura un tanto baja. Su cuerpo entra a una etapa llamada glucólisis, que para no entrar en detalles bioquímicos, diremos que se caracteriza porque el organismo comienza a “producir” (de nuevo, dejemos de lado las formalidades que no aportan nada para nuestro objetivo principal) una cierta cantidad de agua. Dado que esta cantidad producida no entra a nuestro organismo, sino que se genera dentro de él, necesitamos introducir un cuarto término: generación. Nuestro modelo se torna entonces en:

Ese término tiene también su contraparte: así como hay procesos internos que generan una cierta cantidad de agua, también hay procesos como el metabolismo que consumen parte del líquido que deben tomarse en cuenta. Finalmente, nuestra ecuación de balance se convierte en:

Aplicando la mayor cantidad de eventos posibles, podemos hacer un estimado de la cantidad de agua que se quedó dentro del sistema. Ahondemos en algo un tanto más interesante: si en lugar de tomar como sistema el cuerpo humano, que es discontinuo por naturaleza, tomáramos un proceso químico continuo, por decir un reactor, y que siga las mismas características, es decir, que se alimente un flujo de reactivo, que haya un flujo de salida de producto, que exista una generación de producto con su consecuente consumo de reactivo (note usted, estimado lector, que por tratarse de un flujo las unidades se tienen con respecto al tiempo: gramos por hora, galones por minuto, etc) podríamos enfocar nuestro estudio hacia la forma en que varía la cantidad de reactivo dentro del reactor, o la cantidad de producto.

Los mismos conceptos aplicados anteriormente se aplican para el caso de una población. Entiéndase que para una población, las entradas y salidas deben corresponder con los grupos poblacionales que inmigran y emigran, respectivamente; mientras que la generación corresponde con los nacimientos y las salidas corresponden con las muertes. De igual forma, si estas cantidades se expresan con respecto al tiempo se tiene un modelo dinámico que muestra precisamente cómo varía la población en un intervalo definido de tiempo.

Hasta este punto es posible notar que a este sencillo concepto de balancear cantidades pueden añadirse una gran cantidad de términos y variables, aproximando el modelo cada vez más a la población en cuestión. Dejaremos como ejercicio, si el lector así lo cree conveniente, que intente visualizar algunas variables o situaciones que tengan impacto en el crecimiento o decrecimiento de la población en cuestión que no puedan catalogarse en alguna de estas categorías.

Sin embargo, en muchas de las ocasiones no es necesario introducir todos los términos o factores dentro del modelo matemático, simple y sencillamente porque no todos los factores tienen el mismo efecto sobre el caso de estudio. En una gran cantidad de casos experimentales, hay variables que afectan de forma insignificante el resultado del experimento, pero que sí aumentan la dificultad de resolución del modelo matemático, lo que no es justificable desde un punto de vista primariamente económico.

La mejor forma de terminar si existe una relación estadísticamente significativa entre una variable independiente y una variable respuesta, es realizar una correlación. Una correlación indica qué tanto impacto tiene la variación de una variable aleatoria (factor) en otra (resultado). Los métodos utilizados en la estadística clásica cuantifican esta relación en un número que varía entre cero y uno, tomando el valor de cero cuando no existe relación alguna entre las variables y 1 cuando toda la variación de la variable respuesta es debida a una variación en la variable aleatoria independiente.

Volvamos a encaminar nuestra discusión hacia los modelos dinámicos de población. Las aplicaciones de este tipo de modelos son multidisciplinarios, por lo que tienen cabido en una gran cantidad de eventos tanto cotidianos como industriales, de experimentación, etc. Un modelo dinámico de población puede aplicarse, como se vio antes, a un reactor químico para determinar la conversión que presenta, a una torre de destilación para cuantificar la separación que exhibe, a una población humana para evidenciar el crecimiento exponencial que se tiene, a una comunidad de mariposas monarcas para demostrar si se encuentran o no en peligro de extinción, y así podríamos continuar con una gran gama de ejemplos.

Para dar fin a esta tercera sesión, evidenciaré la forma en que varía una población de mariposas monarcas precisamente, que aunque el modelo es algo sencillo, es una excelente forma de comenzar a aplicar los temas discutidos en el post de hoy, y sobre todo de ejemplificarlos.

Modelo Dinámico de la Población de Mariposas Monarcas

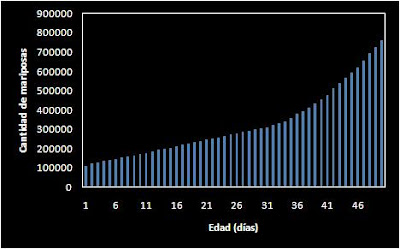
Para preparar el modelo se utilizó una cantidad inicial de 100,000 mariposas y se decidió analizar la variación que presenta la cantidad de mariposas presentes durante este tiempo. Es necesario resaltar, que no se tomaron en cuenta consideraciones como las siguientes:

· No se tomaron en cuenta los riesgos y factores que se tienen durante el viaje que realizan.

· No se considera la posibilidad de que una mariposa que ha sido fecundada puede morir.

· Debido a escasa información acerca del tiempo de gestación, se supuso que una mariposa no podía volver a fecundar durante los 50 días de estudio.

· Se tomaron cantidades fijas promedio para separar las distintas etapas de crecimiento de la mariposa.

Volviendo a lo que sí se consideró, todo parte del balance presentado en la sección anterior. De igual forma, no se consideraron entradas y salidas de mariposas de la colonia, y como factor de generación se tomó la tasa de nacimiento de mariposas; mientras que como evento de consumo se tomó la tasa de muerte de las mismas.

De acuerdo a información obtenida, se decidió catalogar las etapas de crecimiento de todas las mariposas de la misma forma:

Para modelar la cuestión de los nacimientos, se decidió construir una distribución de fertilidad que proporcionara resultados acorde a la realidad, si bien no se realizó en base a experimentación, de forma un tanto empírica se conoce que la forma que debe seguir. Así pues, al acercarse la mariposa a la edad adulta, comienza a incrementarse la probabilidad de que pueda fecundar o ser fecundada, misma probabilidad que se ve maximizada durante su la parte central de su vida media, para después comenzar a disminuir mientras se acerca la etapa denominada “Anciano”.

La distribución construida se presenta en la siguiente figura:

De esta figura se obtiene la probabilidad correspondiente para cada edad, y dado que solo se consideran dos eventos: 1) la mariposa fecunda o es fecundada y 2) la mariposa no fecunda ni es fecundada, se aplicó la teoría de la distribución binomial. El problema consistía entonces en, dada la probabilidad de éxito y contando con la cantidad de sujetos experimentales (cada mariposa que se aparea), calcular la media de las mariposas que fecundan / son fecundadas.

Con esto queda resulta gran parte de la problemática de la tasa de nacimiento, veamos ahora la contracara, la muerte. Para tratar de describir la cantidad de mariposas que mueren, se hizo, de manera análoga, una distribución de probabilidad empírica. Esta distribución representa la probabilidad de vida que tiene cada mariposa, en donde se buscó que la media central estuviera de igual forma en la época temprana de la adultez del sujeto. La distribución construida se presenta a continuación:

De manera semejante, para calcular la tasa de muerte se tienen únicamente dos eventos posibles: 1) la mariposa vive y 2) la mariposa muere. De nueva cuenta la distribución binomial puede aplicarse para encontrar la cantidad de mariposas que mueren dadas las circunstancias de probabilidad de éxito y la cantidad de mariposas existentes.

Ahora, como punto final del diseño, para resolver la ecuación diferencial basada en el balance de individuos, se decidió evaluarla mediante incrementos de un día, que si bien no es la forma más adecuada de hacerlo, son las 3 de la mañana, llevo aquí sentado desde las 4 p.m., y creo que es una buena aproximación de la variación poblacional. El cómo resolver una ecuación diferencial mediante métodos numéricos más exactos ya será cuestión de otro post.

Para finalizar con esta sesión, se presenta la gráfica que representa la forma en que se comporta la variable “cantidad de mariposas” con respecto al tiempo:

Como puede observarse, la población decrece abruptamente conforme aumenta el tiempo de estudio. Este comportamiento se debe principalmente a la distribución de probabilidad de vida construida, ya que quizás los valores sean un tanto bajos o estén distribuidos de manera incorrecta, ya que utilizando una distribución uniforme discreta con una probabilidad cercana a 0.95 se obtiene una gráfica más razonable:

Sin embargo, aún y cuando los resultados no hayan sido los esperados, los propósitos de mostrar la forma de crear un modelo y la concatenación del conocimiento adquirido durante esta tercera sesión de clase con el aprendido durante las sesiones anteriores se llevó a cabo.

El código creado está disponible a través de Google Docs:

http://docs.google.com/Doc?docid=0AUtXURpe4_EeZGRmbjhyZmZfOTRjem12MjZmcg&hl=en