Caso No. 06: A la Cola...

Durante esta sesión se habló acerca de un fenómeno que tiene lugar cuando necesitamos un servicio al mismo tiempo que otras personas: las temibles líneas de espera, o informalmente hablando, las colas. Generalmente a nadie le gusta estar esperando para tomar mesa en algún restaurante, ni a los mismos encargados les gusta tener clientes esperando, ya que cuando la paciencia llega a su límite, estos clientes potenciales se van a comer a otro lugar. En el otro extremo, un servicio demasiado rápido tendría un costo excesivo, por lo que es necesario encontrar un balance adecuado.

Recuerde usted, estimado lector, la sensación tan agobiante que siente cuando necesita cambiar un cheque, o cuando necesita lavar su auto, o cuando necesita entregar alguna papelería y se encuentra con la sorpresa que, antes que usted, existen por lo menos una docena de personas ya esperando. Pero… cómo podemos denominar estas líneas de espera? Y qué significan para nosotros, que gustamos de hablar de la simulación de sistemas?

La primera pregunta es sencilla, una línea de espera es el efecto resultante de un sistema cuando la demanda de un servicio supera la capacidad de proporcionar dicho servicio. Este servicio corresponde entonces con el sistema bajo estudio, y observe el lector que la definición se plantea de tal forma que podemos hacer una retrospectiva al tema dinámica de poblaciones, que a final de cuentas, nos indica la forma en que varía una población, que ahora viene ejemplificada por la línea de espera.

De acuerdo a lo que se propuso en ese entonces, y adaptándolo a esta nueva situación, la línea de espera puede ser modelada mediante términos la ecuación matemática:

En donde el término entrada corresponde con la cantidad demandada del servicio y el término salida indica, a su vez, los servicios que ya han sido satisfechos, mientras que el término acumulación no indica otra cosa que el fenómeno de líneas de espera. Ahora bien, pongamos este tema de discusión, como lo hemos hecho ya en anteriores ocasiones, en un ejemplo que nos sea un tanto más familiar: la caja de un banco cualquiera, a la cual llamaremos caja 1. La diferencia resultante entre la cantidad de gente por unidad de tiempo que llega a esta caja 1 para ser atendida y la cantidad de gente por unidad de tiempo que ya ha sido atendida conforman el lado izquierdo de nuestra igualdad y conforma a su vez la forma en que nuestra línea de espera en la caja 1 aumenta o disminuye con respecto al tiempo. Podríamos entonces, de alguna manera, calcular el tiempo promedio de salida de un cliente que hace una transacción en esta caja y modelar nuestra línea de espera, sabiendo la cantidad de personas que tenemos en nuestra fila.

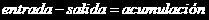
Pero súbitamente, la persona encargada de la caja 2, que casualmente se encontraba en “el tocador”, aparece para aliviar la pesada carga de la caja 1 indicándole a la gente que puede pasar a esta segunda caja recién disponible. Nuestro balance de individuos bajo este supuesto se tornaría en un sistema de ecuaciones, de la siguiente forma:

Esto indica claramente que, tratándose de líneas de espera, cuanto mayor sea la cantidad de etapas en serie (registrarse primero, firmar documentos después y por último pasar con el ejecutivo de cuenta) mayor será el tiempo de salida y por lo tanto el tamaño de la fila será mayor también (efecto comúnmente llamado cuello de botella), mientras que se puede conseguir una disminución en la línea de espera mediante un procesamiento en parelelo (como el caso de abrir una segunda caja en nuestro banco ejemplo, o como los nuevos procesadores de cuatro núcleos). Es evidente que en nuestro sistema, deberíamos de tomar en cuenta en el término salida la cantidad de gente que se pasa de una caja a la otra. De manera semejante a la situación en que solo teníamos una caja disponible, podríamos calcular el tiempo promedio que tarda un cliente en ser atendido en esta segunda caja y utilizarlo en nuestro modelo, con lo que podríamos también modelar el crecimiento en la línea de espera de esta caja 2, siempre y cuando sepamos la cantidad de personas que tenemos en esta segunda fila.

De pronto, aparecen los jóvenes encargados de las cajas 3 y 4, que estaban “echando humo” y comprando una botana con don Lencho, el de las tortas, respectivamente. No hay mayor problema, volvemos a calcular los tiempos promedios en que los clientes son atendidos en estas cajas y agregamos un par de ecuaciones más a nuestro modelo.

Pero entonces nuestra curiosidad toca nuevos límites: qué sucede si la persona encargada de la caja 1 tiene 18 años y es hijo del gerente, mientras que la persona encargada de la caja 3 lleva años en el negocio y se las sabe de todas, todas? Claramente, mientras que la línea de espera de la caja 1 iría en aumento por la lentitud de “el consentido”, la línea de espera de la caja 3 se vaciará rápidamente, estropeando en parte nuestro modelo en donde no suponemos mayores interacciones entre las filas de diferentes cajas.

Como el lector ha de saber, la forma en que los bancos lidian con esta problemática, en un intento por mejorar la distribución de clientes en sus cajas, es la formación de una única línea de espera y el cliente pasa a la caja disponible conforme van terminando los clientes anteriores. Esto, por supuesto, complica en gran parte nuestros cálculos. Aún así, podríamos realizar un análisis de caja negra sobre todas las cajas abiertas, pero dado que tendríamos que calcular un promedio de todos los cajeros, tendríamos un resultado un tanto menos confiable.

Evidentemente entonces, cuando el encargado de dispensar el servicio es un ser humano, al cual llamaremos operador, los tiempos de servicio pueden ser demasiado variables. La cantidad de factores que podrían ocasionar un cambio drástico en el tiempo de servicio humano con respecto al esperado son demasiados, y deben tomarse en cuenta en su gran mayoría. Enseguida se presentan algunos factores que nos dicta la experiencia:

· Factores que varían con el tiempo. La eficiencia del operador puede verse afectada por factores que están en función del tiempo, por ejemplo:

o El cansancio. Claro está que el operador no tiene la misma energía para trabajar a las 10:00 a.m. que a las 5:00 p.m., cuando posiblemente solo esté pensando en su hora de salida.

o La temporada. En lugares de clima templado, las estaciones climáticas afectan en gran medida la eficacia del operador, por ejemplo cuando hace frío.

o La condiciones climáticas. Estas afectan el desenvolvimiento del operador, como por ejemplo en tiempos de lluvia, donde es más probable que el operador se retrase o no se presente por algún accidente.

· Factores independientes del tiempo. La eficiencia del operador puede verse afectada por factores que pueden aparecer en determinadas ocasiones, por ejemplo:

o El fastidio. Después de haber tenido un par de clientes desesperantes, al operador no le quedarán muchas ganas de seguir soportando más clientes.

o Enfermedad. Puede ser que el operador no se presente a trabajar, o si lo hace, es seguro que lo hará más detenidamente.

o La amistad. Puede ser que el operador esté trabajando con algún amigo, con el cual platique de vez en cuando si les toca trabajar lo suficientemente cerca.

En fin, la cantidad de factores que pueden alterar el comportamiento humano es una lista increíblemente grande, lo que torna nuestros cálculos de líneas de espera en modelos incompletos y cuyos resultados son burdas aproximaciones. Sin embargo, la teoría de colas que se desprende de la necesidad de estudiar estas líneas de espera son sumamente importantes para asentar estos modelos. A pesar de los inconvenientes encontrados con la interacción humana, cuando el encargado de proporcionar el servicio es una máquina, la dispersión con que trabaja es menor y los cálculos se aproximan más al escenario real.

Por ejemplo, una máquina que se encarga de poner la tapa en los envases de refresco y que está programada para poner 50 tapas por minuto operará la mayor parte de su tiempo con esta cantidad establecida, por lo que un estudio de colas podrá arrojar resultados reales acerca del comportamiento de los envases que esperan ser tapados. Imagine el lector que si estos resultados fueran una aproximación poco realista, no se podría automatizar este tipo de procesos.

Veamos ahora cómo podríamos estimar los parámetros entrada y salida de las diferentes poblaciones en una línea de espera. El término entrada corresponde entonces a la cantidad de objetos o clientes que llegan al sistema. Dado que no se conoce a ciencias cierta la cantidad de objetos que entran a nuestro sistema, se necesita utilizar un modelo probabilista acorde a la realidad, lo cual aporta la distribución de Poisson, cuya ecuación matemática es:

Esta distribución responde a la incógnita acerca de la probabilidad de que se produzcan x ocurrencias en cierto espacio o tiempo continuo, en donde el promedio de ocurrencias es el único parámetro de esta distribución, λ. En nuestro ejemplo bancario, λ representa la esperanza de llegada de un cliente por unidad de tiempo.

Ahora bien, para nuestro modelo no nos basta con saber la cantidad de objetos que llegarán a nuestro sistema, sino también su “hora de llegada”. Para nuestro ejemplo, no es lo mismo que lleguen 10 clientes en una hora, en donde seguro la fila será larga, a que lleguen los mismos 10 distribuidos durante todo el día, donde seguro no habrá línea de espera, aunque a final de cuenta en ambos eventos tendríamos 10 clientes en un día. Este tiempo que transcurre entre dos llegadas sucesivas a nuestro sistema se denomina tiempo entre llegadas. Como hemos afirmado durante esta nota, los tiempos entre llegada suelen ser demasiado variables en el caso de operaciones en donde no interviene maquinaria. Para modelar la distribución de tiempos entre la presentación de eventos sucesivos (tiempo entre llegadas) se aplica comúnmente la distribución exponencial. Esto principalmente por dos razones: 1) por su capacidad de no tener memoria, con lo que la última llegada no influye en la probabilidad de llegada de la siguiente y 2) debido a que asigna una probabilidad mayor para tiempos de llegada pequeños.

La distribución exponencial tiene como parámetro λ, que aplicado a nuestro ejemplo representa el número esperado de llegadas por unidad de tiempo y recibe por nombre tasa media de llegadas, con unidades de objetos / tiempo. El tiempo esperado entre llegadas corresponde con su inverso 1 / λ.

Es importante señalar que esta distribución responde a la incógnita: cuál es el lapso de tiempo que hay que esperar para que se produzcan x ocurrencias, siendo λ el promedio de ocurrencias? La distribución exponencial tiene su origen al introducir una nueva variable, T(x), que representa el intervalo de tiempo entre ciertas ocurrencias de un suceso de Poisson. T(x) seguirá entonces una distribución exponencial.

Como podrá intuir el lector, existe una relación entre los parámetros de las distribuciones de Poisson y exponencial. Ambas distribuciones se complementan, ya que una mide la cantidad de eventos que tienen lugar durante cierto tiempo y la otra el intervalo de tiempo entre la ocurrencia de estos eventos. Tiene entonces cierta lógica pensar que sus parámetros están relacionados de alguna forma. En efecto, el parámetro λ en la distribución de Poisson mide la tasa media de llegadas durante la unidad de tiempo bajo estudio (que puede ser, para nuestro ejemplo, los 10 clientes por día) mientras que el mismo parámetro en la distribución exponencial mide la misma tasa pero durante un intervalo más específico (que, para nuestro ejemplo, puede ser la distribución de los 10 clientes durante la mañana y ningún cliente por la tarde).

Veamos esto con un ejemplo sencillo: en nuestro banco, supongamos que se sabe, por datos históricos, que entre las 10:00 a.m. y las 12:00 p.m. (2 horas) llegan en promedio 6 clientes. Si se requiere calcular la probabilidad de que entre las 10:30 y las 11:30 (1 hora) ingresen 4 clientes, aplicamos la distribución de Poisson:

Supongamos ahora que, para el mismo proceso, necesitamos calcular la probabilidad de que el primer cliente llegue después de las 11:45 a.m. (1/4 hora), dado que se sabe que en promedio entra al banco un cliente cada 20 minutos (1/3 hora). Aplicamos esta vez la distribución exponencial:

Para modelar el tiempo de salida, y a sabiendas de que se necesita una distribución de los tiempos entre la presentación de tiempos sucesivos, se puede aplicar la misma distribución exponencial.

En resumen, la descripción aquí mencionada es importante al momento de querer simular una línea de espera, situación que ocurre cuando se quiere optimizar o hacer más eficiente la toma de decisiones con respecto a ella. Por ejemplo, cómo saber si uno como gerente necesita contratar a un cajero más para saber si con esto realmente se disminuyen las filas? No sería conveniente, por varias razones, contratar a una persona para hacer estas pruebas y si no funciona despedirlo. O, en cambio, podría ser necesario evaluar la opción de recortar a uno de los cajeros sin perjudicar la longitud promedio de la fila? Y si esto es factible, a cuál de los cajeros necesito despedir? En fin, en todas estas situaciones hipotéticas en donde es necesario saber de antemano la respuesta antes de tomar una decisión, la simulación de líneas de espera se vuelve no solo importante, sino vital.

Las aplicaciones de simulación de líneas de espera se encuentran prácticamente en todas las disciplinas, desde un proceso químico, en donde una línea de espera podría ser un efluente de reactivo que espera su turno de entrar a un reactor, hasta una tortillería en donde los clientes tienen que hacer fila para poder comprar sus tortillas, pasando por un sinfín de fenómenos en la naturaleza.

Quisiera cerrar esta nota con las leyes de Harper sobre las líneas de espera, que a pesar que no todos las conocemos o estamos familiarizados con ellas, nos rigen cada día de nuestras vidas:

1ª Ley de Harper: No importa la cola en que se sitúe, la otra siempre avanzará más rápido.

2ª Ley de Harper: Si decide cambiarse de cola, aquella en que estaba al principio empezará a ir más deprisa.

Ya la deducción será tema de otro día!